|
|
|
Hydrological Theory
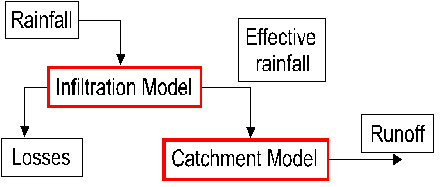
Rainfall runoff models may be grouped in two general classifications that are illustrated in Figures 7-16 and 7-17. The first approach uses the concept of effective rainfall in which a loss model is assumed which divides the rainfall intensity into losses and an effective rainfall hyetograph. The effective rainfall is then used as input to a catchment model to produce the runoff hydrograph. It follows from this approach that the infiltration process ceases at the end of the storm duration.
Figure 7-16 - A rainfall-runoff models using effective rainfall. An alternative approach that might be termed a surface water budget model, incorporates the loss mechanism into the catchment model. In this way, the incident rainfall hyetograph is used as input and the estimation of infiltration and other losses is made as an integral part of the calculation of runoff. This approach implies that infiltration will continue to occur as long as the average depth of excess water on the surface is finite. Clearly, this may continue after the cessation of rainfall.
Figure 7-17 – A rainfall-runoff model using a surface water budget MIDUSS allows you the option to use particular implementations of both these techniques. The effective rainfall approach is employed in a convolution algorithm that uses response functions of different shape. For the case of triangular or rectangular response functions the time base is computed by a kinematic wave equation which involves the intensity of the effective rainfall. The convolution process is therefore nonlinear in that the response function changes throughout the storm but the principle of superposition is retained. These two approaches are embodied in the ‘Rectangular’ and ‘Triangular SCS’ options of the Hydrology/Catchment command. The third convolution option uses a response function which is obtained by routing a rectangular input of duration Dt and height A/Dt through a linear reservoir with a lag or storage coefficient KL=tc/2. For this case, the time of concentration tc is computed using the kinematic wave equation [7-41] but for the maximum value of effective rainfall intensity. An example of a surface water budget model is also made available in the form of the SWMM/RUNOFF algorithm and can be implemented by using the ‘SWMM method’ option. It is important to note that if the ‘SWMM method’ option is to be employed it is necessary to use the Horton or Green and Ampt infiltration models to represent the rainfall losses. The four options are described in the sections that follow.
|
|||
|
|
|||
|
(c) Copyright 1984-2023 Alan A. Smith Inc. |
|
|